Question 1.
Answer the following:
i) How many dimensions a solid has ?
Solution:
A solid has three dimensions namely length, breadth and height or depth.
ii) How many books are there in Euclid’s Elements ?
Solution:
There are 13 volumes in Euclid’s elements.
iii) Write the number of faces of a cube and cuboid.
Solution:
Cube : 6 faces
Cuboid : 6 faces
iv) What is the sum of interior angles of a triangle ?
Solution:
The sum of interior angles of a triangle is 180°.
v) Write three undefined terms of geometry.
Solution:
Point, line and plane are three undefined terms in geometry.
Question 2.
State whether the following statements are true or false. Also give reasons for your answers.
- a) Only one line can pass through a given point
- b) All right angles are equal
- c) Circles with same radii are equal
- d) A finite line can be extended on its both sides endlessly to get a straight line
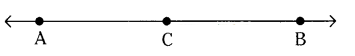
e) From figure AB > AC
Solution:
a) Only one line can pass through a given point - False.
Reason : (Since, infinitely many lines can pass through a given point)
b) All right angles are equal - True.
c) Circles with same radii are equal - True.
d) A finite line can be extended on its both sides endlessly to get a straight line - True.
e) From figure AB > AC - True.
Question 3.
In the figure given below, show that the length AH > AB + BC + CD.

Solution:
Given a line AH↔
To prove AH > AB + BC + CD
From the figure AB + BC + CD = AD
AD is a part of whole AH.
From Euclid’s axiom whole is greater than part.
∴ AH > AD
⇒ AH > AB + BC + CD
Question 4.
If a point Q lies between two points P and R such PQ = QR, prove that PQ = 1/2 PR.

Let PR be a given line.
Given that PQ = QR
i. e., Q is a point on PR.
⇒ PQ + QR = PR
⇒ PQ + PQ = PR [∵ PQ = QR]
⇒ 2PQ = PR
⇒ PQ = 1/2 PR
Hence proved.
Question 5.
Draw an equilateral triangle whose sides are 5.2 cm
Soluton:
- Step 1 : Draw a line segment AB of length 5.2 cm. *
- Step 2 : Draw an arc of radius 5.2 cm with centre A.
- Step 3 : Draw an arc of radius 5.2 cm with centre B.
- Step 4 : Two arcs intersect at C; join C to A and B.
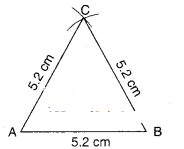
Δ ABC is the required triangle.
Question 6.
What is a conjecture? Give an example for it.
Solution:
Mathematical statements which are neither proved nor disproved are called conjectures. Mathematical discoveries often start out as conjectures. This may be an educated guess based on observations.
Eg : Every even number greater than 4 can be written as sum of two primes. This example is called Gold Bach Conjecture
Question 7.
Mark two points P and Q. Draw a line through P and Q. Now how many lines are parallel to PQ, can you draw ?
Solution:
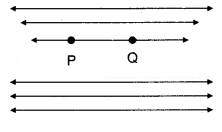
Infinitely many lines parallel to PQ can be drawn.
Question 8.
In the figure given below, a line n falls on lines / and m such that the sum of the interior angles 1 and 2 is less than 180°, then what can you say about lines l and m ?
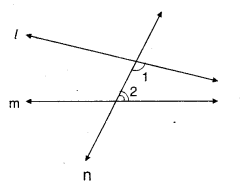
Solution:
Given : l, m and n are lines, n is a transversal.
∠1 < 90°
∠2 < 90°
If the lines l and m are produced on the side where angles 1 and 2 are formed, they intersect at one point.
Question 9.
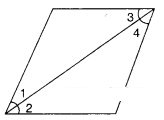
In the figure given below, if ∠1 = ∠3, ∠2 = ∠4 and ∠3 = ∠4 write the rela-tion between ∠1 and ∠2 using Euclid’s postulate.
Solution :
Given : ∠1 = ∠3
∠3 = ∠4
∠2 = ∠4
∴∠1 = ∠2
∵Both ∠1 and ∠2 are equal to ∠4. (By Euclid’s axiom things which are equal to same things are equal to one another).
Question 10.
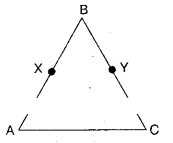
In the figure given below, we have BX = 1/2 AB, BY= 1/2 BC and AB = BC. Show that BX = BY.
Solution:
Given : BX = 12 AB
BY = 12BC
AB = BC
To prove : BX = BY
Proof: Given AB = BC [ ∵ By Euclid’s axiom things which are halves of the same things are equal to one another]
12 AB = 12 BC
BX = BY
Hence proved.